Lazy Segment Tree

이 글은 segment tree(이하 segtree)를 완벽히 이해했음을
전제로 진행하는 글입니다.
Segment tree

Segment Tree

 

왜 필요한가요?

segtree는 특정 원소를 수정하는 데 $O(logN)$의 시간복잡도가 소요됩니다.
그러나 특정 원소가 아닌, 특정 구간에 해당하는 모든 원소를 수정할 경우
시간복잡도는 $O(LlogN)$으로 매우 커지게 됩니다.
lazy segment tree는 이를 $O(logN)$에 처리하게 해주는 스킬입니다.

lazy segment tree

 

먼저, 위에 적힌 배열을 누적합 segtree로 도식화 해봤습니다.
이제 (1, 6) 구간에 2를 더해봅시다.
(1, 6) 범위를 segtree에서 표현하려면 (1, 4) + (5, 6)만으로 표현됩니다.
(1, 1), (2, 2), ..., (6, 6)까지 내려갈 필요가 없는 것이죠.

 

그러니, 'lazy'하게 적당히만 내려가봅시다.

 

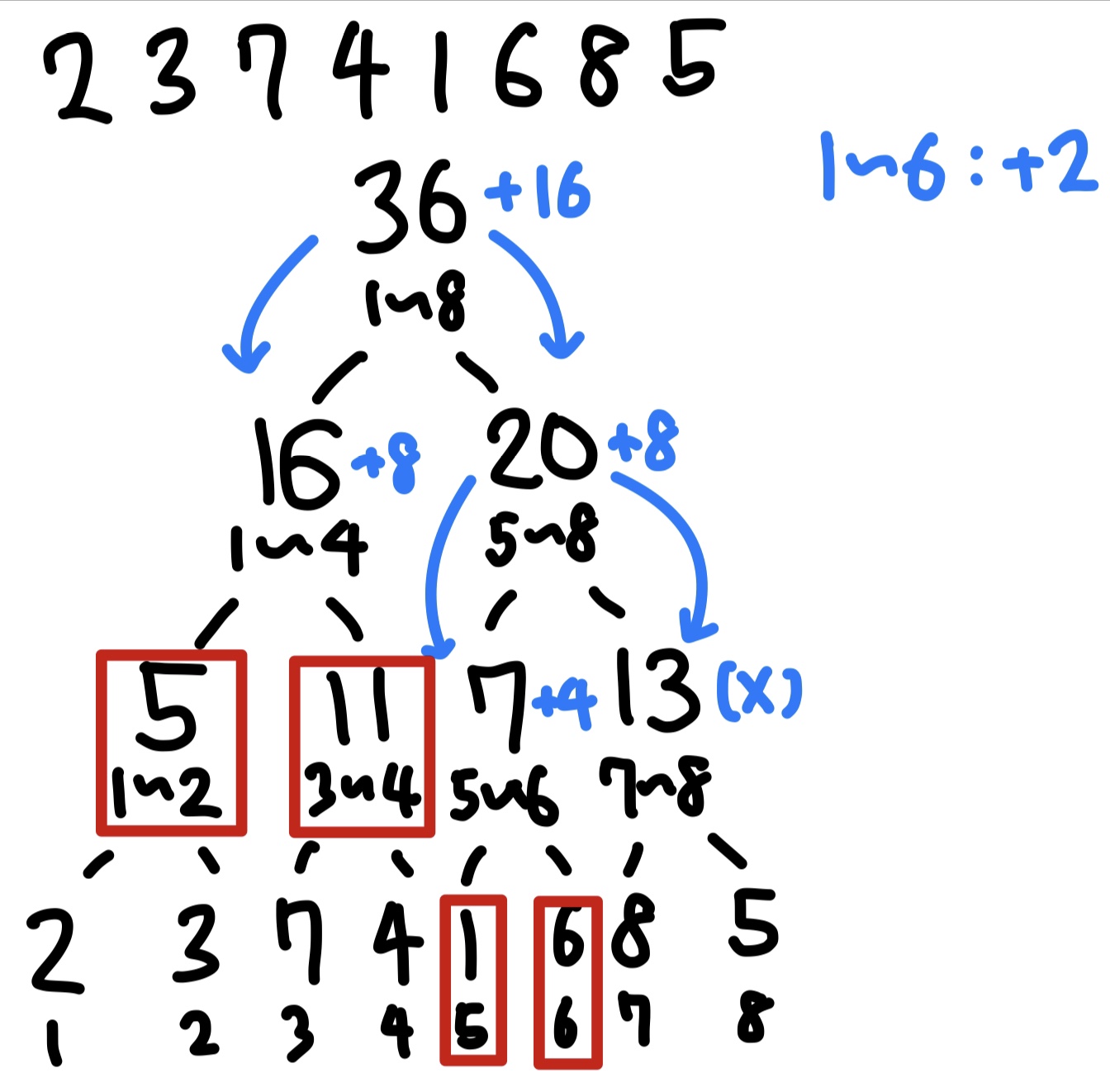
위 그림의 파란색 경로까지만 진행하면, (1, 6)의 부분합을 구하는 과정과
유사하기에 시간복잡도는 $O(logN)$입니다.
그러나 실제로는 더 내려갔었어야 합니다.
예를 들어, (1, 4) 구간까지만 내려가도 (1, 6)을 표현할 수 있지만
실제로는 (1, 2), (3, 4) 구간도 수정을 해야하죠.
그렇기에 (1, 2), (3, 4) 구간에는 전체 구간 +2 쿼리를 진행해야 하지만
아직 반영하지는 않았다는 의미에서 lazy 배열에 2씩 더해줍니다.
(5, 6) 구간도 마찬가지로 (5, 6)만으로 (1, 6)을 표현할 수 있지만
실제로는 (5, 5), (6, 6) 구간도 전체 구간 +2 쿼리를 진행해야 하기에
lazy 배열에 2씩 더해주면 됩니다.

void edit(int now, int s, int e, int f, int r, int x)
//now: tree 배열에 저장할 번호, s, e: 현재 관리할 배열의 시작/끝 값
//f, r: 값을 더할 구간의 시작/끝 값, x: 값을 바꿀 원소에 더할 값
{
    if (r < s || e < f) return;
    //범위가 안맞을 경우 return
    if (f <= s && e <= r) {
        tree[now] += x*(e-s+1);
        //범위가 완전히 포함된 경우 우선 더하기
        lazy[now<<1]+=x; lazy[now<<1|1]+=x;
        //현재 노드 밑의 노드들은 나중에 처리, lazy에 저장
        return;
    }
    int mid = s+e >> 1;
    edit(now<<1, s, mid, f, r, x);
    edit(now<<1|1, mid+1, e, f, r, x);
    tree[now] = tree[now<<1] + tree[now<<1|1];
    //범위가 애매할 경우 반반 나눠 결과의 합 저장
}

 

lazy에 저장해놓은 정보들은 언제 반영할까요?
lazy 값이 존재하는 범위까지 고려하여 쿼리를 진행해야 할 때입니다.
이 경우, 이전에 있던 lazy 값들을 단순히 더해주고,
위에서와 마찬가지로 현재 lazy 값들을 밑으로 내려주면 됩니다.
그 후 반영한 lazy 값은 초기화해주면 됩니다.
이런 행위를 push라 하면, push는 수정, 범위 합을 구하는 함수의 맨 처음에
해당 범위의 lazy 값이 0이 아니라면 진행하면 됩니다.

전체 코드는 다음과 같습니다.

void push(int now, int s, int e)  
{  
    tree[now] += lazy[now]*(e-s+1);  
    if (s ^ e) {
        lazy[now<<1] += lazy[now];  
        lazy[now<<1|1] += lazy[now];  
    }
    lazy[now] = 0;  
}  

void edit(int now, int s, int e, int f, int r, int x) 
{  
    if (lazy[now]) push(now, s, e);
    if (r < s || e < f) return;
    if (f <= s && e <= r) {  
        tree[now] += x*(e-s+1);
        lazy[now<<1]+=x; lazy[now<<1|1]+=x;
        return;
    }  
    int mid = s+e >> 1;  
    edit(now<<1, s, mid, f, r, x);  
    edit(now<<1|1, mid+1, e, f, r, x);  
    tree[now] = tree[now<<1] + tree[now<<1|1]; 
}

문제 적용

12844번 문제의 예시 코드입니다.
XOR

12844번: XOR

 

xor 비트연산자의 특징을 고려한다면 어렵지 않게 이해할 수 있습니다.

 

#include <bits/stdc++.h>
using namespace std;

int N, Q, a[500005], tree[2000005], lazy[2000005];

void push(int now, int s, int e)
{
    if ((s&1) == (e&1)) tree[now] ^= lazy[now];
    if (s ^ e) {lazy[now<<1] ^= lazy[now]; lazy[now<<1|1] ^= lazy[now];}
    lazy[now] = 0;
}

void mt(int now, int s, int e)
{
    if (s == e) {tree[now] = a[s]; return;}
    int mid = s+e >> 1;
    mt(now<<1, s, mid); mt(now<<1|1, mid+1, e);
    tree[now] = tree[now<<1] ^ tree[now<<1|1];
}

void edit(int now, int s, int e, int f, int r, int v)
{
    if (lazy[now]) push(now, s, e);
    if (r < s || e < f) return;
    if (f <= s && e <= r) {
        lazy[now] ^= v;
        if (lazy[now]) push(now, s, e);
        return;
    }
    int mid = s+e >> 1;
    edit(now<<1, s, mid, f, r, v); edit(now<<1|1, mid+1, e, f, r, v);
    tree[now] = tree[now<<1] ^ tree[now<<1|1];
}

int ans(int now, int s, int e, int f, int r)
{
    if (lazy[now]) push(now, s, e);
    if (r < s || e < f) return 0;
    if (f <= s && e <= r) return tree[now];
    int mid = s+e >> 1;
    return ans(now<<1, s, mid, f, r) ^ ans(now<<1|1, mid+1, e, f, r);
}

int main()
{
    cin.tie(0)->sync_with_stdio(0);
    cin>>N;
    for (int i = 1; i <= N; i++) cin>>a[i];
    mt(1, 1, N);
    cin>>Q; while (Q--) {
        int t, x, y, z; cin>>t>>x>>y;
        if (t&1) {cin>>z; edit(1, 1, N, x+1, y+1, z);}
        else cout<<ans(1, 1, N, x+1, y+1)<<"\n";
    } return 0;
}